Generative Adversarial Networks (GANs) and CycleGANs

Introduction

Generative Adversarial Networks (GANs) have emerged as a groundbreaking approach in generative modeling using deep learning techniques. Introduced by Ian Goodfellow and his colleagues in 2014, GANs have revolutionized the way we generate synthetic data.

What are GANs?

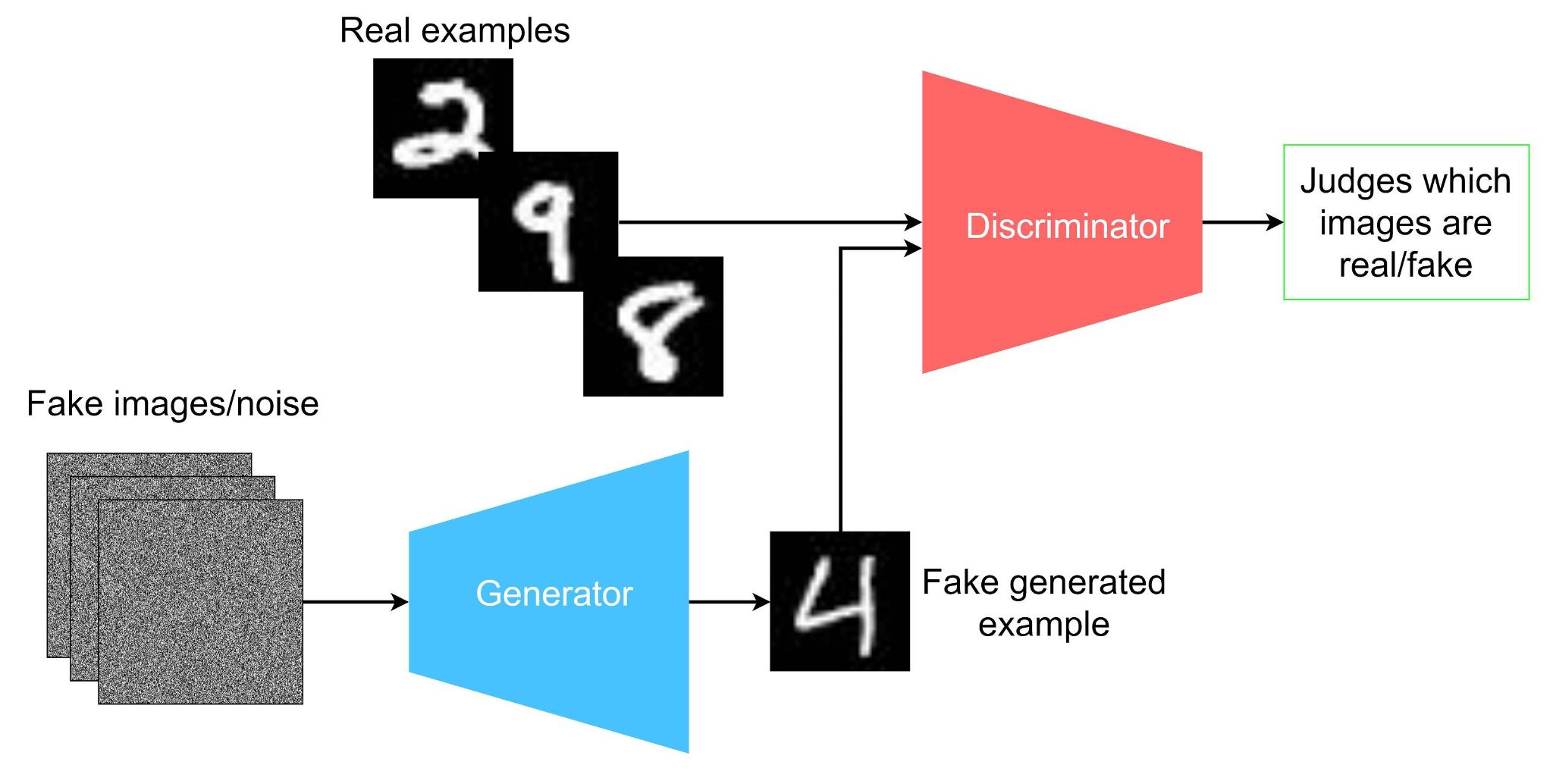
Generative Adversarial Networks (GANs) designed to generate realistic data by training two neural networks, the generator and the discriminator, in a competitive setting. The generator creates synthetic data, while the discriminator evaluates the authenticity of the data, distinguishing between real and fake samples.

Components of GANs

1. Generator: This network generates new data instances that resemble the training data.

2. Discriminator: This network evaluates the authenticity of the data, distinguishing between real and generated instances.

The generator aims to produce data that is indistinguishable from real data, while the discriminator tries to identify whether the data is real or generated. The two networks are trained together in a zero-sum game, improving each other iteratively.

Structure of GANs

GANs consist of two main parts:

• Generative: The generator takes random noise as input and generates synthetic data.

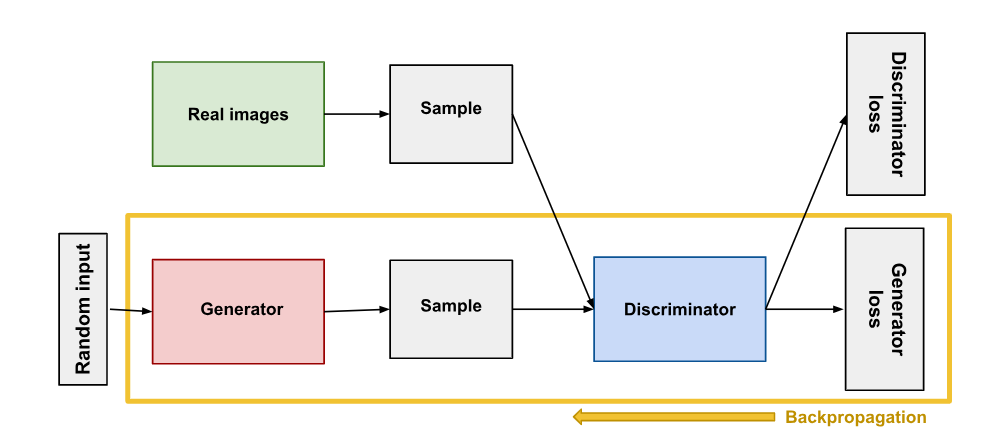
• Adversarial: The discriminator tries to distinguish between real data and synthetic data produced by the generator.

Mathematical Formulation

The training of GANs involves the following objective functions for the generator and discriminator:

• Discriminator Loss:

$$ L_D = - \mathbb{E}_{x \sim p_d(x)}[\log D(x)] - $$

$$ \mathbb{E}_{z \sim p_z(z)}[\log (1 - D(G(z)))] $$

• Generator Loss: $$ L_G = - \mathbb{E}_{z \sim p_z(z)}[\log D(G(z))] $$

where:

• ( $D(x)$ ) is the discriminator’s estimate of the probability that real data instance ( $x$ ) is real.
• ( $G(z)$ ) is the generator’s output given noise ( $z$ ).
• ( $p_{d}(x)$ ) is the real data distribution.
• ( $p_z(z)$ ) is the prior distribution on input noise variables.

Consider a simple GAN to generate handwritten digits similar to the MNIST dataset:

1. Generator Network: Takes random noise as input and generates a 28x28 image.
2. Discriminator Network: Takes a 28x28 image as input and outputs a probability score indicating whether the image is real or fake.

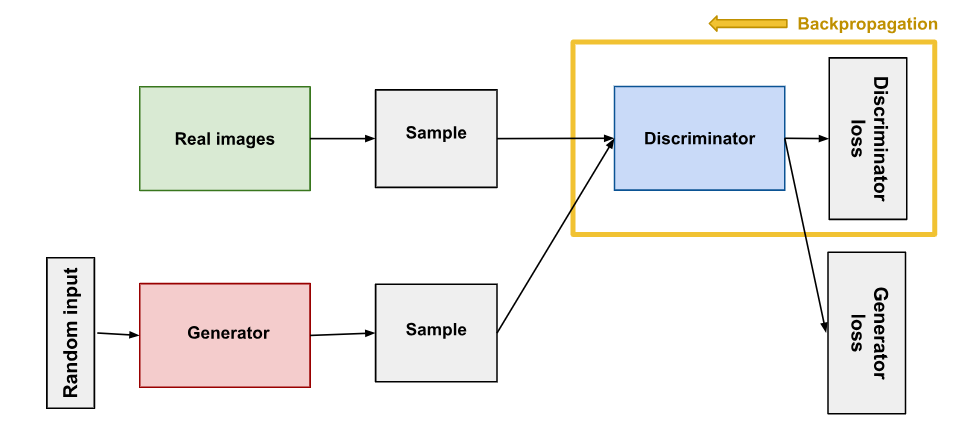
The networks are trained iteratively:

1. Train the discriminator on real and fake images.
2. Train the generator to produce images that can fool the discriminator.

CycleGAN

CycleGANs are a variant of GANs designed for image-to-image translation without requiring paired examples. They are particularly useful for tasks where paired training data is unavailable.

Structure of CycleGANs

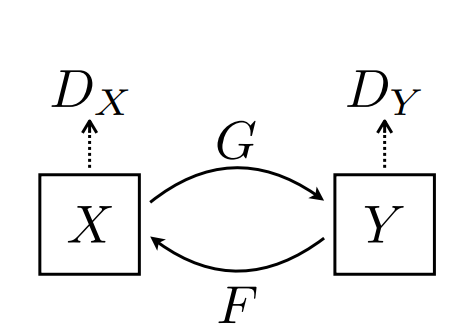
CycleGANs consist of two sets of generators and discriminators:

• Generators: $( G: X \to Y )$ and $( F: Y \to X )$
• Discriminators: $( D_Y )$ and $( D_X )$, which evaluate the realism of generated images.

Loss Functions in CycleGANs

1. Adversarial Loss:

$$ L_{GAN}(G, D_Y, X, Y) = \mathbb{E}_{y \sim p_d(y)}[\log (D_Y(y))] + $$

$$ \mathbb{E}_{x \sim p_d(x)}[\log (1 - D_Y(G(x)))] $$

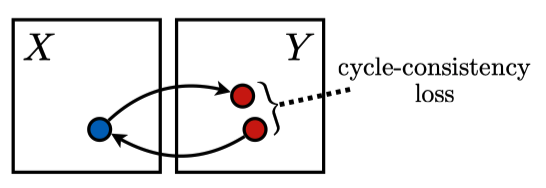
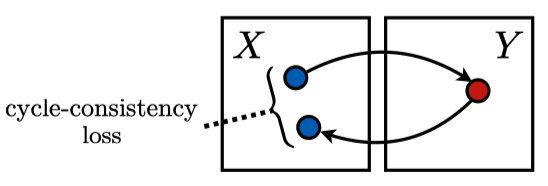
2. Cycle-Consistency Loss:

$$ L_{cyc}(G, F) = \mathbb{E}_{x \sim p_d(x)}[| F(G(x)) - x |_1] + $$

$$ \mathbb{E}_{y \sim p_d(y)}[| G(F(y)) - y |_1] $$

3. Total Loss: $$ L(G, F, D_X, D_Y) = L_{GAN}(G, D_Y, X, Y) + L_{GAN}(F, D_X, Y, X) + \lambda L_{cyc}(G, F) $$

where $( \lambda )$ is a weight parameter that balances the two loss functions.

Example

Consider translating images from the domain of horses to the domain of zebras:

1. Generator $( G )$: Transforms horse images to zebra images.
2. Generator $( F )$: Transforms zebra images to horse images.
3. Discriminator $( D_Y )$: Evaluates whether an image is a real zebra or generated by $( G )$.
4. Discriminator $( D_X )$: Evaluates whether an image is a real horse or generated by $( F )$.

The training process involves:

1. Minimizing the adversarial loss to ensure the generated images are indistinguishable from real images.
2. Minimizing the cycle-consistency loss to ensure the content of the images is preserved during the translation.