Introduction
The Transformer architecture, introduced in the seminal paper “Attention Is All You Need” by Vaswani et al. in 2017, has revolutionized the field of natural language processing (NLP) and beyond with its key innovation: the Attention mechanism.
The Transformer Architecture
Overview
The Transformer is a neural network architecture designed to handle sequential data, particularly in tasks like machine translation, text summarization, and language understanding. Unlike its predecessors (RNNs and LSTMs), Transformers process entire sequences simultaneously, allowing for more parallelization and, consequently, faster training on larger datasets.
To understand why this is revolutionary, consider how we typically process language. Traditionally, we’d look at words one by one, trying to understand each in the context of what came before. Transformers, however, look at the entire sentence at once, weighting the importance of each word in relation to all the others. This is akin to understanding the meaning of a sentence by considering all words simultaneously rather than sequentially.
The architecture consists of two main components:
- Encoder: Processes the input sequence
- Decoder: Generates the output sequence
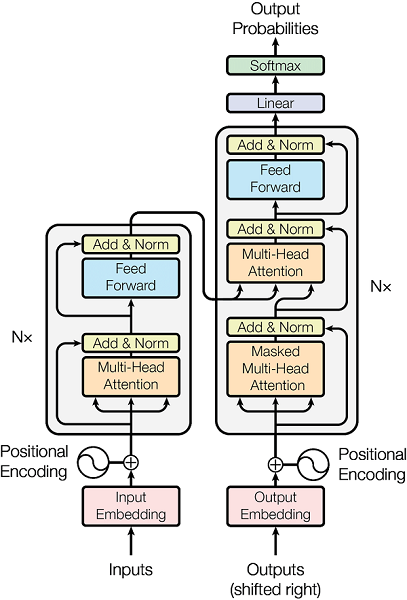
Both the encoder and decoder are composed of a stack of identical layers, each containing two sub-layers:
- Multi-Head Attention mechanism
- Position-wise Fully Connected Feed-Forward Network
Key Components
1. Input Embedding
Before processing, input tokens (which could be words or subwords) are converted into continuous vector representations. This is typically done using learned embeddings. Mathematically, this can be represented as:
$E = XW_e$
Where:
- $E$ is the embedding matrix
- $X$ is the one-hot encoded input
- $W_e$ is the learned embedding weight matrix
This formula represents the process of mapping discrete tokens to continuous vector spaces. Each row of $W_e$ corresponds to the embedding vector for a specific token in the vocabulary.
Why is this important? Words (or tokens) in language don’t inherently have mathematical meaning. By converting them to vectors, we’re representing them in a way that captures semantic relationships. For instance, in a well-trained embedding space, the vectors for “king” and “queen” might be close to each other, reflecting their related meanings.
2. Positional Encoding
One key difference between Transformers and traditional sequence models is that Transformers don’t inherently understand the order of the input sequence. To address this, we add positional encodings to the input embeddings. This injects information about the position of tokens in the sequence.
The positional encoding is calculated using sine and cosine functions:
$PE_{(pos,2i)} = \sin(pos / 10000^{2i/d_{model}})$ $PE_{(pos,2i+1)} = \cos(pos / 10000^{2i/d_{model}})$
Where:
- $pos$ is the position in the sequence
- $i$ is the dimension
- $d_{model}$ is the embedding dimension
Why use sine and cosine functions? These functions have a beautiful property: for any fixed offset k, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$. This allows the model to easily learn to attend to relative positions, which is crucial for understanding language structure.
This encoding allows the model to distinguish between different positions in the sequence. Without it, the model would treat “The cat sat on the mat” and “The mat sat on the cat” identically, which would be problematic for understanding meaning!
3. Multi-Head Attention
This is the core innovation of the Transformer architecture, explained in the next section. The key idea is that it allows the model to focus on different parts of the input when producing each part of the output, much like how we might focus on different words when translating a sentence.
4. Feed-Forward Networks
Each attention layer is followed by a position-wise feed-forward network. This consists of two linear transformations with a ReLU activation in between:
$FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2$
Where:
- $x$ is the input to the feed-forward network
- $W_1$, $W_2$ are weight matrices
- $b_1$, $b_2$ are bias vectors
This feed-forward network is applied to each position separately and identically. It allows the model to introduce non-linearity and increase the representational power of the network. The ReLU activation helps in learning complex patterns.
Why is this necessary? The attention mechanism is inherently linear. By adding this non-linear feed-forward network, we’re giving the model the ability to approximate more complex functions, which is crucial for learning intricate patterns in language.
5. Layer Normalization and Residual Connections
After each sub-layer (attention and feed-forward), layer normalization is applied. Additionally, residual connections are used around each sub-layer:
$LayerNorm(x + Sublayer(x))$
Layer normalization helps stabilize the learning process by normalizing the inputs across the features. The residual connections allow for deeper networks by providing a direct path for gradients to flow backwards, mitigating the vanishing gradient problem.
This combination of normalization and residual connections is crucial for training very deep networks. It helps the model learn stably even with many layers, which is key to the power of large language models like GPT-3.
The Attention Mechanism
Intuition
The attention mechanism is the heart of the Transformer architecture. But what exactly is Attention? In essence, it’s a way for the model to focus on different parts of the input when producing each part of the output.
Think about how you read a complex sentence. You don’t give equal importance to all words; you focus more on some words to understand the overall meaning. That’s essentially what attention does for the model.
Scaled Dot-Product Attention
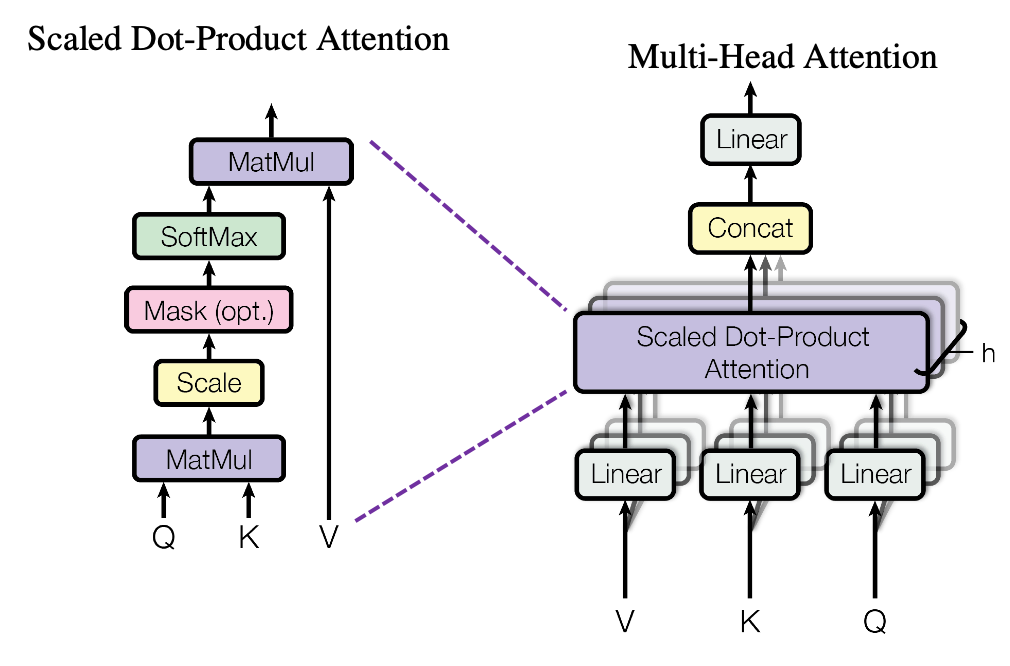
The basic building block of attention in Transformers is called Scaled Dot-Product Attention. It’s defined as:
$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
Where:
- $Q$: Query matrix
- $K$: Key matrix
- $V$: Value matrix
- $d_k$: Dimension of the keys
Let’s break this down step by step:
- Compute the dot product of the query with all keys: $QK^T$. This gives us a measure of how much each key should be attended to for this particular query.
- Scale the result by $\sqrt{d_k}$ to counteract the effect of large dot products in high dimensions. Without this scaling, for large values of $d_k$, the dot products get large, pushing the softmax function into regions where it has extremely small gradients.
- Apply a softmax function to obtain the weights on the values. This converts the scores to probabilities, ensuring they sum to 1.
- Multiply the values by their corresponding weights from the softmax. This gives us a weighted sum of the values, where the weights determine how much each value contributes to the output.
The intuition here is that we’re deciding how much to attend to different parts of the input (represented by the keys and values) based on what we’re looking for (the query).
Multi-Head Attention
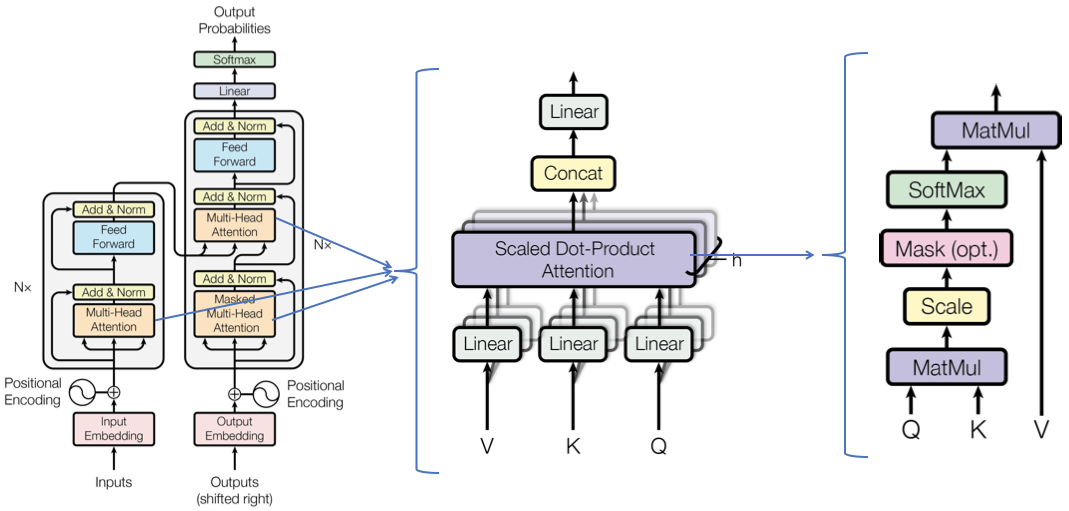
Instead of performing a single attention function, the Transformer uses multi-head attention. This allows the model to jointly attend to information from different representation subspaces at different positions.
Multi-head attention consists of several attention layers running in parallel:
$MultiHead(Q, K, V) = Concat(head_1, …, head_h)W^O$
where $head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)$
Here, the $W$ matrices are learned parameters. Each head can learn to attend to different aspects of the input, allowing for a richer representation.
Why is this useful?
Different heads can learn to focus on different aspects of the relationship between words. One head might learn to focus on syntactic relationships, while another might focus on semantic relationships. This multi-faceted approach allows the model to capture a more nuanced understanding of the input.
Types of Attention in Transformers
-
Encoder Self-Attention: Each position in the encoder attends to all positions in the previous encoder layer. This allows each token to gather information from all other tokens in the input sequence.
-
Decoder Self-Attention: Each position in the decoder attends to all previous positions in the decoder. This is made causal (masked) to prevent positions from attending to subsequent positions, which is necessary for autoregressive generation.
-
Encoder-Decoder Attention: Each position in the decoder attends to all positions in the encoder. This allows the decoder to focus on relevant parts of the input sequence for each decoding step.
These different types of attention allow the model to capture various types of relationships within and between sequences, enabling it to perform complex language tasks.
Mathematical Deep Dive
Let’s break down the mathematics of the attention mechanism even further:
-
Query, Key, and Value Calculation: For each attention head $i$:
$Q_i = XW_i^Q$ $K_i = XW_i^K$ $V_i = XW_i^V$
Where $X$ is the input, and $W$ matrices are learned parameters. This linear transformation allows each head to project the input into a different subspace, enabling the model to capture different types of relationships in the data.
-
Attention Scores:
$S_i = \frac{Q_iK_i^T}{\sqrt{d_k}}$
This computes a similarity score between each query and key. The scaling factor $\sqrt{d_k}$ prevents the dot products from growing too large in magnitude, which could push the softmax function into regions with very small gradients.
-
Attention Weights:
$A_i = softmax(S_i)$
The softmax function normalizes the scores, converting them into a probability distribution. This determines how much each value will contribute to the output. The softmax ensures that the weights sum to 1 for each query.
-
Output of Each Head:
$H_i = A_iV_i$
This weighted sum of the values represents the output of each attention head. It combines the values based on the attention weights, allowing the model to focus on relevant information for each position.
-
Concatenation and Final Projection:
$MultiHead = Concat(H_1, …, H_h)W^O$
The outputs of all heads are concatenated and projected to the desired dimension using another learned weight matrix $W^O$. This final step combines the information from all attention heads into a single representation.
This mathematical formulation allows the model to dynamically focus on different parts of the input for each part of the output, enabling it to capture complex relationships in the data.
Why Transformers Work So Well?
-
Parallelization: Unlike RNNs, Transformers can process entire sequences in parallel, leading to faster training. This is because the self-attention operation can be computed for all positions simultaneously.
-
Long-range Dependencies: The attention mechanism allows the model to directly connect distant positions, mitigating the vanishing gradient problem that plagued RNNs. Every output element is connected to every input element, and the weighted sum of these connections is what allows the model to easily learn long-range dependencies.
-
Flexible Context: By using attention, the model can dynamically focus on relevant parts of the input, regardless of their position. This is particularly useful in tasks like translation, where the order of words might change between languages.
-
Rich Representations: Multi-head attention allows the model to capture different types of relationships in the data simultaneously. Each head can specialize in different aspects of the input, providing a more comprehensive representation.
-
Interpretability: The attention weights can be visualized to understand which parts of the input the model is focusing on for each output. This provides some level of interpretability, which is often lacking in deep neural networks.
-
Scalability: The architecture of Transformers scales well with more data and larger model sizes. This has led to the development of increasingly large and powerful models like GPT-3 and BERT.
The Transformer architecture and its attention mechanism have become the backbone of many state-of-the-art models in NLP and beyond. Their ability to process sequential data efficiently while capturing complex relationships has led to breakthroughs in various applications. As research continues, we’re seeing Transformers adapted for vision tasks, multi-modal learning, and even scientific applications like protein folding prediction. Understanding the fundamentals of this architecture is crucial for anyone working in modern machine learning and artificial intelligence.